本地英文版地址: ../en/search-aggregations-pipeline-movavg-aggregation.html
[6.4.0] 在6.4.0版本中废弃。 移动平均聚合已被弃用,取而代之的是更通用的移动函数(moving function)聚合。 新的移动函数聚合提供了与移动平均聚合相同的功能,但也提供了更多的灵活性。
给定一系列有序的数据,移动平均聚合将在数据上滑动一个窗口,并得出该窗口的平均值。
例如,给定数据[1, 2, 3, 4, 5, 6, 7, 8, 9, 10],我们可以计算窗口大小为5的简单移动平均值,如下所示:
- (1 + 2 + 3 + 4 + 5) / 5 = 3
- (2 + 3 + 4 + 5 + 6) / 5 = 4
- (3 + 4 + 5 + 6 + 7) / 5 = 5
- 等等...
移动平均是平滑连续数据的一种简单方法。 移动平均通常应用于基于时间的数据,如股票价格或服务器指标。 平滑可用于消除高频波动或随机噪声,这使得低频趋势更容易被可视化,如季节性。
一个单独的moving_avg看起来像这样:
{
"moving_avg": {
"buckets_path": "the_sum",
"model": "holt",
"window": 5,
"gap_policy": "insert_zeros",
"settings": {
"alpha": 0.8
}
}
}
表 18. moving_avg参数
| 参数名称 | 描述 | 是否必需 | 默认值 |
|---|---|---|---|
|
感兴趣的度量的路径 (更多详情请参考 |
必需 |
|
|
我们希望使用的移动平均加权模型 |
可选 |
|
|
确定当遇到数据中的间隙时应该发生什么 |
可选 |
|
|
在直方图上“滑动”的窗口大小 |
可选 |
|
|
模型是否应该在算法上最小化。更多细节请参考最小化 |
可选 |
大多数模型用 |
|
特定于模型的设置,内容根据指定的模型而有所不同。 |
可选 |
moving_avg聚合必须嵌入一个histogram或date_histogram聚合中。
它们可以像任意其他度量聚合一样嵌入:
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg":{
"moving_avg":{ "buckets_path": "the_sum" }
}
}
}
}
}
|
名为“my_date_histo”的 |
|
|
|
|
|
最后,我们指定一个 |
移动平均的构建,首先要指定一个字段的histogram或date_histogram。
然后,你可以选择在直方图中添加一个常用的度量,比如sum。
最后,moving_avg 被嵌入直方图中。
然后,buckets_path参数用于“指向”直方图内的一个同级指标(有关buckets_path语法的描述,请参见buckets_path语法)。
来自上述聚合的示例响应可能如下所示:
{
"took": 11,
"timed_out": false,
"_shards": ...,
"hits": ...,
"aggregations": {
"my_date_histo": {
"buckets": [
{
"key_as_string": "2015/01/01 00:00:00",
"key": 1420070400000,
"doc_count": 3,
"the_sum": {
"value": 550.0
}
},
{
"key_as_string": "2015/02/01 00:00:00",
"key": 1422748800000,
"doc_count": 2,
"the_sum": {
"value": 60.0
},
"the_movavg": {
"value": 550.0
}
},
{
"key_as_string": "2015/03/01 00:00:00",
"key": 1425168000000,
"doc_count": 2,
"the_sum": {
"value": 375.0
},
"the_movavg": {
"value": 305.0
}
}
]
}
}
}
moving_avg聚合包括四种不同的移动平均“模型”。
主要区别在于窗口中的值是如何加权的。
随着窗口中的数据点变得“更老”,它们的权重可能会有所不同。
这将影响该窗口的最终平均值。
模型使用参数model来指定。
某些模型可能有可选配置,这些配置在其参数settings中指定。
simple模型计算窗口中所有值的总和,然后除以窗口的大小。
它实际上是窗口的简单算术平均值。
simple模型不执行任何时间相关的加权,这意味着simple移动平均值的值往往会“滞后”於真实数据。
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg":{
"moving_avg":{
"buckets_path": "the_sum",
"window" : 30,
"model" : "simple"
}
}
}
}
}
}
simple模型没有需要配置的特殊设置。
窗口大小可以改变移动平均线的行为。
例如,一个小窗口(比如"window": 10)将密切跟踪数据,只平滑小范围的波动:
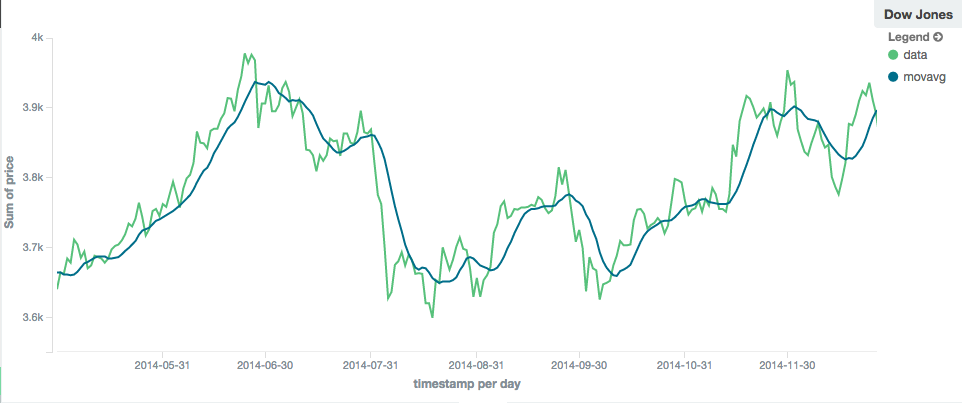
相反,一个有更大窗口(比如"window": 100)的simple移动平均线,它会消除所有高频的波动,只留下低频的长期趋势。
它还会“滞后”实际数据一大截:

linear模型给序列中的点分配一个线性加权,
这样“较老”的数据点(例如,窗口开始的那些)对总平均值的贡献线性减少。
线性加权有助于减少数据均值的“滞后”,因为较老的点的影响较小。
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg": {
"moving_avg":{
"buckets_path": "the_sum",
"window" : 30,
"model" : "linear"
}
}
}
}
}
}
linear模型没有需要配置的特殊设置。
像simple模型一样,窗口大小可以改变移动平均线的行为。
例如,一个小窗口(比如"window": 10)将密切跟踪数据,只平滑小范围的波动:
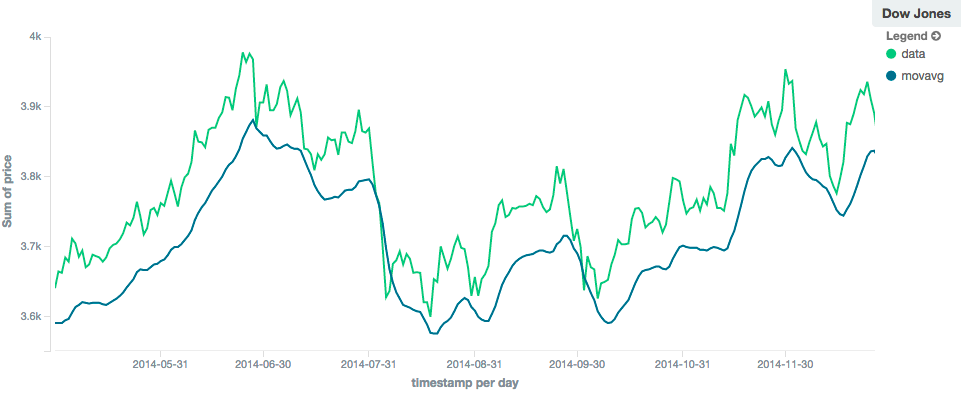
相比之下,具有较大窗口(比如"window": 100)的linear移动平均线将消除所有高频波动,只留下低频的长期趋势。
它还还是倾向于“滞后”实际数据一个相当大的量,尽管通常比simple模型要少:

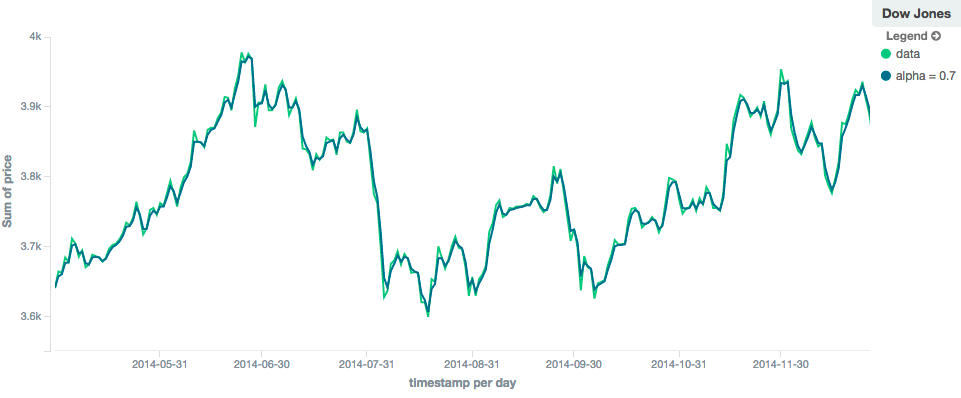
ewma模型(又名“单指数”)类似于linear模型,不同的是,旧的数据点的重要性是以指数级降低,而不是线性降低。
重要性衰减的速度可以通过设置alpha来控制。
较小的值使权重缓慢衰减,这提供了更大的平滑度,并考虑了窗口的更大部分。
较大的值会使权重迅速衰减,从而降低较旧值对移动平均线的影响。
这往往会使移动平均线更密切地跟踪数据,但却不太平滑。
alpha的默认值为0.3,该设置接受0-1之间的任何浮点数。
EWMA模型可以最小化
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg": {
"moving_avg":{
"buckets_path": "the_sum",
"window" : 30,
"model" : "ewma",
"settings" : {
"alpha" : 0.5
}
}
}
}
}
}
}

holt模型(亦称作“二次指数”)结合了跟踪数据趋势的第二个指数项。
当数据具有潜在的线性趋势时,单指数表现不佳。
二次指数模型在内部计算两个值:“水平(level)”和“趋势(trend)”。
水平(level)计算类似于ewma,是数据的指数加权视图。
不同之处在于,使用了之前平滑的值,而不是原始值,这使其接近原始序列。
趋势(trend)计算着眼于当前值和上一个值之间的差异(例如,平滑数据的斜率或趋势)。
趋势值也是指数加权的。
数值是由水平(level)分量和趋势(trend)分量相乘产生的。
alpha的默认值为0.3,beta的默认值为0.1。
该设置接受0-1之间的任意浮点数。
holt-linear 模型可以最小化
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg": {
"moving_avg":{
"buckets_path": "the_sum",
"window" : 30,
"model" : "holt",
"settings" : {
"alpha" : 0.5,
"beta" : 0.5
}
}
}
}
}
}
}
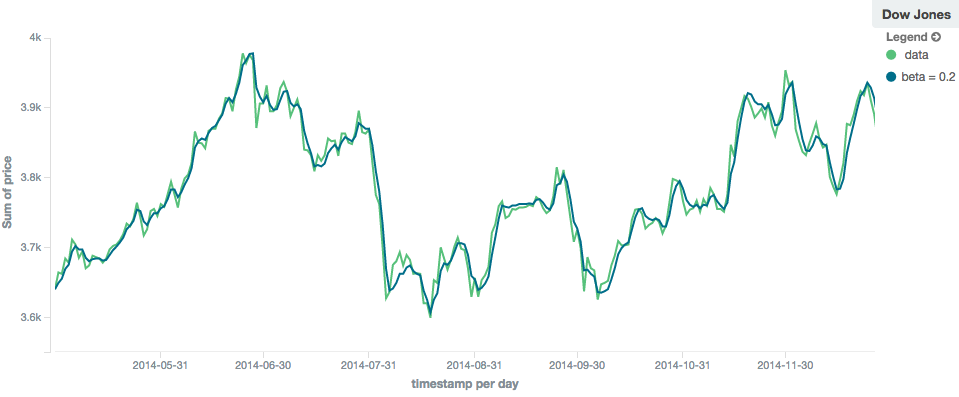
实际上,alpha值在holt模型中的表现与在ewma模型中非常相似:小值产生更多平滑和更多滞后,而大值产生更密切的跟踪和更少的滞后。
beta的值往往很难看出。
较小的值强调长期趋势(例如整个系列中的恒定线性趋势),而较大的值强调短期趋势。
当你预测价值时,这一点会变得更加明显。
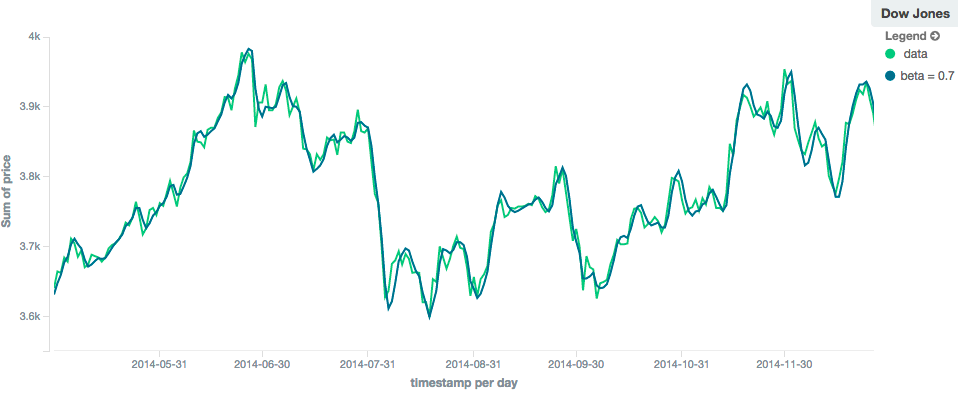
holt_winters模型(又名“三级指数”)包含第三个指数项,用于跟踪数据的季节性。
因此,这种聚合基于三个要素进行平滑:“水平(level)”、“趋势(trend)”和“季节性(seasonality)”。
水平(level)和趋势(trend)计算与holt里的相同。
季节性(seasonal)计算着眼于当前点与前一时段点之间的差异。
与其他移动平均线相比,holt-winters 需要更多的操作。
你需要指定数据的“周期(periodicity)”:例如,如果你的数据每7天有一个循环趋势,可以设置period: 7。
类似地,如果有月趋势,你可以把它设置为30。
目前没有周期性检测,尽管计划在未来进行增强。
holt-winters 有两种类型: additive(加法)和multiplicative(乘法)。
不幸的是,由于 holt-winters 的性质,它需要两个周期(period)的数据来“引导”该算法。
这意味着你的window值必须至少是周期(period)的两倍。
如果不是,将会抛出异常。
这也意味着holt-winters不会为第一个2 * period桶生成值;当前算法不进行回溯。
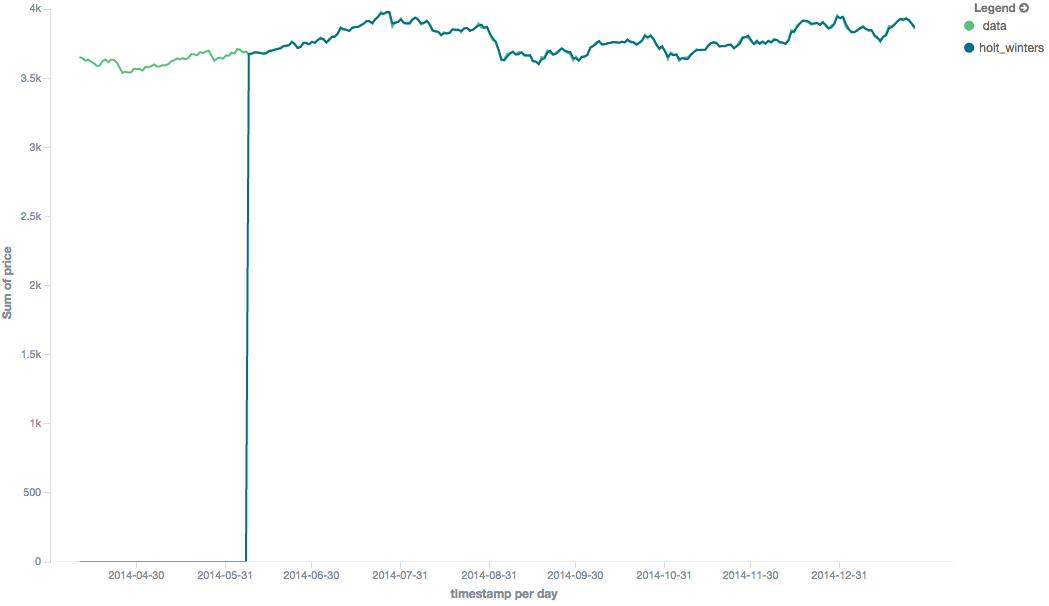
因为“冷启动”掩盖了移动平均线的样子,所以Holt-Winters图像的其余部分被截断以不显示“冷启动”。 请注意,这将永远出现在移动平均线的起点!
加法季节性是默认的;也可以通过设置"type": "add"来指定。
当季节性影响添加到数据中时,这种变化是首选的。
例如,你可以简单地减去季节性影响,将你的数据“去季节性化”成一个平坦的趋势。
alpha和gamma的默认值是0.3,而beta是0.1。
这些设置接受0-1之间的任意浮点数。
period的默认值是1。
additive holt-winters 模型可以最小化
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg": {
"moving_avg":{
"buckets_path": "the_sum",
"window" : 30,
"model" : "holt_winters",
"settings" : {
"type" : "add",
"alpha" : 0.5,
"beta" : 0.5,
"gamma" : 0.5,
"period" : 7
}
}
}
}
}
}
}
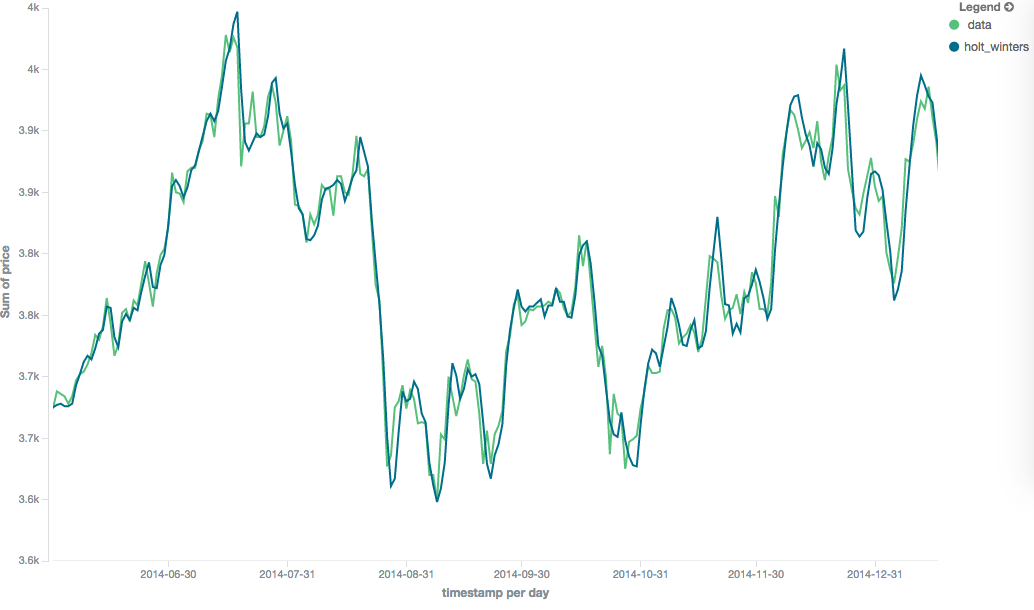
乘法通过设置"type": "mult"来指定。
当季节性影响与数据相乘时,这种变化是首选。
例如,如果季节性影响是数据的5倍,而不是简单地增加它。
alpha和gamma的默认值是0.3,而beta是0.1。
这些设置接受0-1之间的任意浮点数。
period的默认值是1。
multiplicative holt-winters 模型可以最小化
乘法霍尔特-温特斯的工作原理是将每个数据点除以季节值。
如果任何数据为零,或者数据中有间隙(因为这会导致除以零),那么这就有问题了。
为了解决这个问题,mult Holt-Winters用一个非常小的量(1*10-10)填充所有的值,这样所有的值都是非零的。
这会影响结果,但影响很小。
如果你的数据是非零的,或者你希望在遇到零时看到NaN,则可以使用pad: false禁用此行为
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg": {
"moving_avg":{
"buckets_path": "the_sum",
"window" : 30,
"model" : "holt_winters",
"settings" : {
"type" : "mult",
"alpha" : 0.5,
"beta" : 0.5,
"gamma" : 0.5,
"period" : 7,
"pad" : true
}
}
}
}
}
}
}
此功能是试验性的,在未来的版本中可能会被更改或完全删除。 Elastic将尽最大努力解决任何问题,但实验功能不受官方GA功能的支持SLA的约束。
所有移动平均模型都支持“prediction(预测)”模式,该模式将尝试在给定当前平滑移动平均的情况下推断未来。 根据模型和参数的不同,这些预测可能准确,也可能不准确。
通过向任何移动平均聚合添加一个predict参数,指定要追加到序列末尾的预测数,可以启用预测。
这些预测将按照与桶相同的间隔排列:
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg": {
"moving_avg":{
"buckets_path": "the_sum",
"window" : 30,
"model" : "simple",
"predict" : 10
}
}
}
}
}
}
simple、linear和ewma模型都产生“扁平的”预测:它们基本上收敛于序列中最后一个值的平均值,产生平坦的预测:
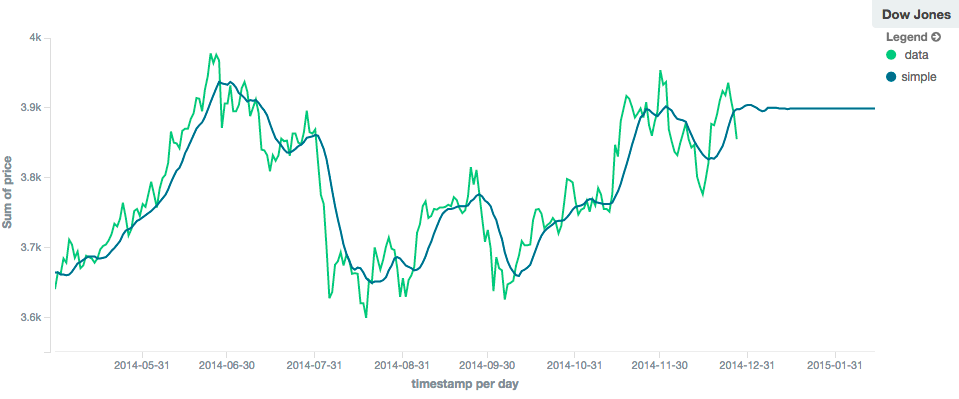
相比之下,holt模型可以根据局部或全局的恒定趋势进行推断。
如果我们设置一个较高的beta值,则可以根据局部的恒定趋势进行推断(在这种情况下,预测是向下的,因为系列末尾的数据是向下的):
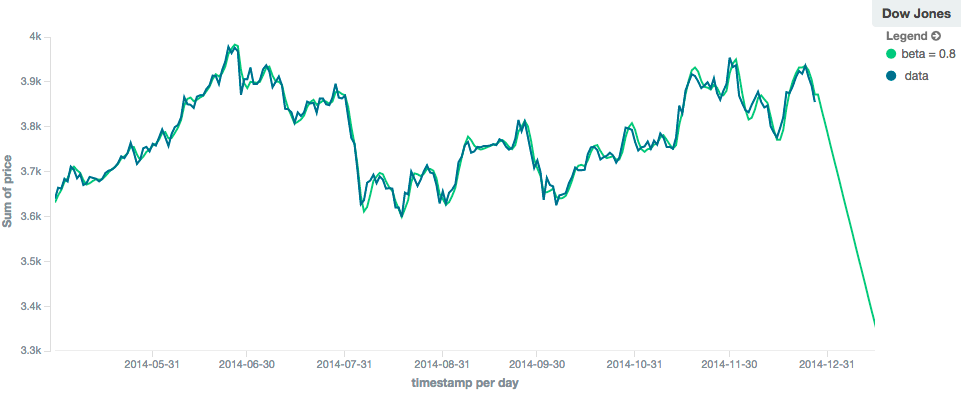
相比之下,如果我们选择一个小的beta值,预测是基于全局不变的趋势。
在这一系列中,全局趋势略显积极,因此预测做了一个急转弯,开始了一个正斜率:

holt_winters模型具有提供最佳预测的潜力,因为它还将季节性波动纳入了模型:
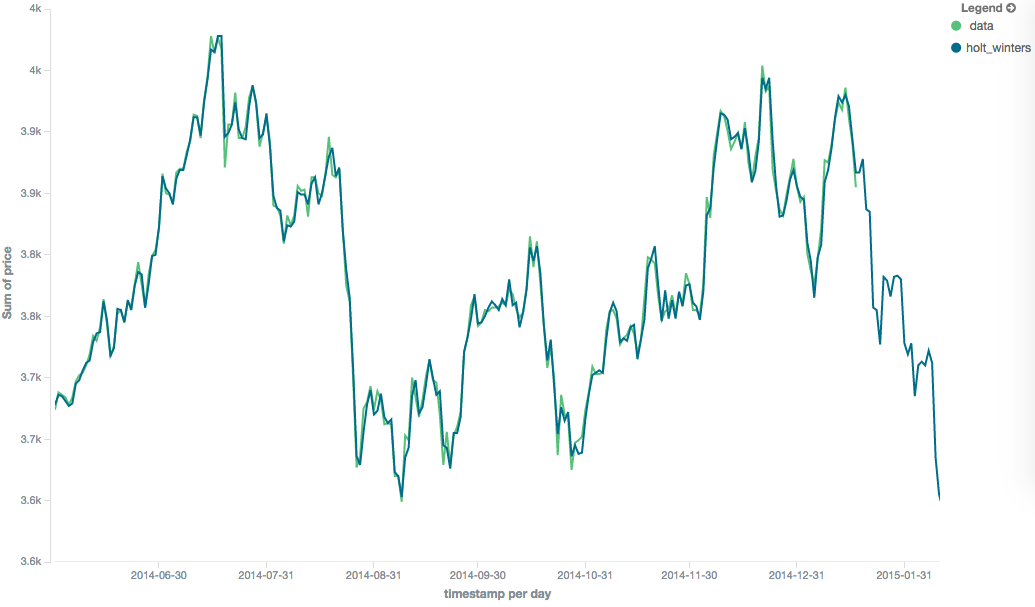
一些模型(EWMA, Holt-Linear, Holt-Winters)需要配置一个或多个参数。 参数选择可能很棘手,有时不直观。 此外,这些参数的微小偏差有时会对输出的移动平均值产生巨大影响。
出于这个原因,这三个“可调”模型可以在算法上最小化。 最小化是一个调整参数的过程,直到模型生成的预测与输出数据高度匹配。 最小化并不是完全可靠的,而且容易受到过度拟合的影响,但它通常会比手动调优提供更好的结果。
ewma和holt_linear模型默认禁用了最小化,而holt_winters模型则默认启用了最小化。
最小化对holt_winters最有用,因为它有助于提高预测的准确性。
ewma和holt_linear主要用于平滑数据,但不是很好的预测工具,因此最小化在这两个模型上用处不大。
通过minimize参数启用/禁用最小化:
POST /_search
{
"size": 0,
"aggs": {
"my_date_histo":{
"date_histogram":{
"field":"date",
"calendar_interval":"1M"
},
"aggs":{
"the_sum":{
"sum":{ "field": "price" }
},
"the_movavg": {
"moving_avg":{
"buckets_path": "the_sum",
"model" : "holt_winters",
"window" : 30,
"minimize" : true,
"settings" : {
"period" : 7
}
}
}
}
}
}
}
启用时,最小化将找到alpha、beta和gamma的最佳值。
用户仍然应该为window、period和type提供适当的值。
最小化的工作原理是运行一个叫做simulated annealing(模拟退火)的随机过程。 这个过程通常会产生一个好的解决方案,但不能保证找到全局最优解。 它还需要一些额外的计算能力,因为随着值的调整,模型需要重新运行多次。 最小化的运行时间与窗口大小成线性关系:过大的窗口可能会导致延迟。
最后,最小化将模型拟合到最后n个值,其中n = window。
这通常会对未来产生更好的预测,因为参数是在系列结束时调整的。
但是,它可能会在系列开始时生成较差的拟合移动平均线。